姑且是准备入 PhD 坑了，基础的东西更需要好好复习。本文的内容会覆盖西瓜书第三章的内容。在线性模型的部分， MLPR 里头学的一些东西也会尽量地放进来。上次看到某学弟的深度学习入门文章写得很不错，要么尝试一下转变文风吧(

背景故事：穿越到异世界的召唤师

你穿越到了一个异世界。

在落地的一阵晕眩后，你努力地试图理解发生了什么：你研究生毕业，单身，在某大手IT会社工作半年。长年累月的月月火水木金金的学习工作让你变强了，也变秃了。虽然你还单身，天天被隔壁的美工与销售嘲讽，但是只要再忍一忍就有望转职成能手搓火球的大魔法师，有着光明的未来。这天，你被老板派遣去某个客户那里进行一些现场工作，但是你刚出门就被一道白光所笼罩……

不管怎么说，你来到了这个世界，也没有短时间能回去的迹象。在这个新世界生存下来是当务之急的第一任务。这个世界有大量的迷宫一般的地下城，地下城里除了或凶猛或狡猾的魔物，还有大量的素材，矿物，草药等等高价物品的出产。因此，冒险者经济蓬勃发展。战士，法师，牧师，暗牧，弓箭手……各种各样的职业冒险家组成队伍探索地下城。当他们返回地上时，往往带着大包小包的商品。为了照顾冒险家的需求，地下城的附近如雨后春笋一般冒出了旅馆、酒馆、教会、道具店等各种各样的设施。不知运气好是不好，你刚好落在了一个由于地下城而形成的聚居地。

按照你熬夜打游戏看小说的经验，一般来钱的方法要么就是到地下城打怪挖宝，然后卖东西；要么就是拥有类似钓鱼，狩猎之类的生产技能，能够通过销售生产的物资来赚钱。你打开了技能栏，显然的，由于在穿越之前过着一日三餐靠外卖，每天上班996的生活，生产技能可是一个也没有。而在职业技能栏，大大的“召唤师”三个字把你转职成大魔法师的希望一扫而空，而翻遍了整个技能栏，你能找到的只有“召唤史莱姆”这么一个技能。

一般来说，召唤师在哪里都是职业鄙视链最底层的存在：召唤出来的魔物要么弱智不堪，需要召唤者发号施令，浪费精力，抓不住时机；要么就完全不可操控，自行其是，搞乱整个战场，痛击队友。更何况，史莱姆也是魔物界最弱鸡的存在。但是眼下也没有其他办法，总之先把史莱姆召唤出来，先挣点钱保证生存再说。

在好一阵鸡飞狗跳过后，你好不容易带着你的史莱姆拳打南山哈比幼儿园，脚踢北海哥布林敬老院，再加上捡其他冒险者落下的素材武器，好不容易凑出了能够生存几天的费用。在旅馆里，你一边碎碎念于刚才被奸商狠宰的一笔面包钱，一边鼓捣着自己的那只弱鸡史莱姆，左戳戳，右戳戳，看看能不能改善一下它在战斗中跟睡着了一样毫无反应的问题。不知怎么的，史莱姆突然瘫成了一滩水一样的平面。你赶紧打开手边那本《召唤师入门大全》，希望能够找到问题所在。

看了半天你看不懂但是莫名其妙能明白的文字，你突然明白了你召唤的史莱姆是一种特别珍稀的可控制史莱姆。这只史莱姆的攻击防御跟其他的史莱姆没什么不同，但是可以通过一个线性函数来控制它攻击的时机与力道。而你，在穿越之前，正好是项目组里的机器学习担当。这意味着，虽然能力相同，但是你完全可以靠着控制史莱姆的攻击与防御来实现更好的攻击效率。另一方面，现有的机器学习模型能够帮你解决一些现实问题—比如，如何防止再次掉入奸商的面包价格陷阱。

“什么嘛，我学到的东西果然还是有用的嘛！”你这么想着。只要不停下来，机器学习之道就会向前延伸——

第三章线性模型

机器学习的普遍形式

如果我们从更高一层次的角度来思考机器学习，我们大致可以将机器学习定义成通过样本的特征，通过学习器，输出标签的过程。其中，通过不断地更新学习器，我们可以提升机器学习的表现（正确率等）。在史莱姆模型中，我们的任务可以定义如下：

样本的特征: 影响补给品的价格的因素，比如面包的类型（黑面包，白面包等），今日回城的冒险者数量，面包的日产量，历史价格等，用不同数量的石子输入
输出标签：补给品的价格，用石子表示
学习器：弱小可怜但能吃的史莱姆，吃进代表样本特征的石头，吐出代表标签的石头。史莱姆的状态可以通过喂食不同的草药进行调整

除此之外，我们需要一个损失函数来衡量我们的学习器距离目标有多“远”。这个目标可以是正确的标签，也可以是另外的衡量标准等。我们还需要一个优化器，来将我们的学习器调整到正确的状态。对于史莱姆模型而言：

损失函数：我们要衡量我们预测的价格跟正确的价格之间的差距
优化器：你自己，通过不断地喂食来改变史莱姆的状态。

线性模型的基本形式

线性模型是最基本的机器学习模型之一。线性模型认为，我们需要的标签是输入特征的线性组合：给定每个输入特征以某个权重，输出标签由这些权重与相应特征值的加权所决定。令 $f$ 为模型， $w$ 为参数， $x$ 为样本的特征，我们可以将线性模型简单地表示如下：

$f(x_1, x_2, ... x_n) = w_1 x_1 + w_2 x_2 + ... + w_n x_n + b$

其中 $b$ 是截距。

根据输出标签的种类划分，机器学习有两大任务：

回归任务，输出的标签是一个连续值，例如补给品的价格。
分类任务，输出的标签是一个离散值，例如明天是否会下雨等。

线性模型可以解决这两个方面的问题。根据故事中的你的需求，我们先来看看如何解决预测补给品价格这种回归类问题。

线性回归

线性回归使用线性模型的加权值作为预测的标签，即上文的函数 $f$ 的函数值。线性回归的目标是求得一组恰当的权重( $w$ , $b$ )，
从而使得函数 $f$ 能够尽可能准确地输出预测值。换句话说，我们希望函数的预测值 $f(x)$ 与真实的标签 $y$ 之间
的“距离”最小。一般而言，在线性回归任务中，我们使用均方误差函数来衡量这个“距离”：

$J(\theta) = \sum_{i=0}^N (f(x_i) - y_i)^2$

其中 $\theta$ 指模型的参数，在线性回归即指的是权重 w 与截距 b。注意到均方误差同欧氏距离有着紧密的联系，从可解释性的角度来说，均方误差很直观地表现了“距离目标有多远”这个概念。因此，只要使均方误差函数最小，我们就可以得到一个最优化的预测函数。通过最小化均方误差来获得最优的参数的方法被称作最小二乘法。

史莱姆模型：线性回归预测面包的价格

现在，你回忆起了线性回归的相关知识，但是由于你的能力还比较弱小，你决定先用面包的价格来测试一下构建史莱姆模型是否可行。已知面包的价格由面包的重量，种类，店家等因素影响。你想先用一个一元线性回归模型来预测一下面包的重量与价格的关系。于是，你定义机器学习任务如下：

输入特征：面包的重量，种类，店家……
输出标签：面包的价格
学习器：线性模型
损失函数：均方误差函数
优化器：在这个阶段，你决定先用手动调节的方式进行调参。

按照这个要求，你从收集的价格数据里面摘出参数如下：

重量(x)	价格(y)
100	25
200	35
300	45
50	20
150	32
250	39
350	51
99	25
199	35
299	44
399	53

现在，你需要调整史莱姆的状态，使得损失函数的值在面包数据集上最小。为了简单清晰起见，我们用数学的方式表示出来：

$\begin{aligned} \min J(w, b) &= \sum_i^N (y_i - f(x_i))^2\\ &= \sum_i^N (y_i - w x_i - b)^2 \end{aligned}$

根据基本的微积分知识（谢天谢地，你还记得导数是什么），很显然的，对于一个二次函数而言，导数为 0 的时候有最值，而我们的损失函数显然是一个开口向上的二次函数，也就是说导数为 0 的时候有最小值。对于多元函数而言（这里的元是权重与截距，而不是 x, y)，二次多元函数的每个分量取偏导数为 0 的时候有最小值。对这个函数我们可以列方程如下：

$\begin{aligned} \frac{\partial J}{\partial w} &= 2(w \sum_i x_i^2 + \sum_i(b - y_i)x_i) = 0\\ \frac{\partial J}{\partial b} &= 2(Nb + \sum_i(wx_i - y_i)) = 0 \end{aligned}$

解方程可得:

$\begin{aligned} w &= \frac{\sum_i(y_i - \overline y)x_i}{\sum_i (x_i - \overline x)x_i}\\ b &= \overline y - w \overline x \end{aligned}$

在变量上加横线如 $\overline y$ 这样的形式来表示平均值。

代入面包数据，计算可得 w = 0.096, b = 15.75。剩下的工作，就是不断试错调整史莱姆的状态

截距与多元线性回归

经过一番九牛二虎之力，你终于搞定了权重 w 与截距 b。但是，你希望有一种更加简洁，统一的方式来表示权重与截距。

一种最简单的方式：每次喂给史莱姆一个常数值“1”，这样子史莱姆每次都会输出定值。写成公式表示如下：

$\begin{aligned} f(x) &= w_1 x_1 + w_2 x_2\\ x_1 &= x\\ x_2 &= 1 \end{aligned}$

现在，你发现了权重跟截距都有统一的表达方式，也就是说，可以用同一种方式调♂教截距与权重了。你又发现，如果需要增加一个特征的话，你可以很简单地增加一个权重，即 $wx$ 项。根据你回忆起的知识，这叫做多元线性回归。

不用尝试，你也知道如果特征不断增加，你你将会调整一大堆权重的情况，一个个解方程显然非常累。你想到了用矩阵的方式来表述这个公式：

$\begin{aligned} f(\mathbf{x}) &= \mathbf{w}^T\mathbf{x} =\sum_j w_j x_j\\ \mathbf{w} &= \left [\begin{matrix} w_1 \\ w_2 \\ ... \\ b \end{matrix}\right]\\ \mathbf{x} &= \left [\begin{matrix} x_1\\ x_2\\ ...\\ 1 \end{matrix}\right]\\ \end{aligned}$

这里 $T$ 表示矩阵的转置，一般用列向量统一表示权重向量与特征向量。这样带来的一个好处是，如果使用一个二维矩阵 $\mathbf{x}$ 来表示整个数据集，我们可以简单地表示将函数作用于整个数据集所得到的向量：

$\mathbf{y}' = \mathbf{X}\mathbf{w} = \left[ \begin{matrix} f(x_1)\\ f(x_2)\\ ...\\ f(x_N) \end{matrix}\right]$

目标函数也因为矩阵表述变成了这样子：

$J(\theta=\mathbf{w}) = (\mathbf{y} - \mathbf{X}\mathbf{w})^T(\mathbf{y} - \mathbf{X}\mathbf{w})$

通过对权重进行求导（注：求导方法以后会讨论），我们可以得到如下方程：

$\frac{\partial J}{\partial \mathbf{w}} = 2\mathbf{X}^T(\mathbf{X}\mathbf{w} - \mathbf{y})$

由于这里涉及到矩阵的逆运算，有这么几种情况：

a) 当矩阵 $\mathbf{X}^T\mathbf{X}$ 是满秩矩阵或者正定矩阵，则逆矩阵存在，解方程可得解析解

$\mathbf{w} = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}$

b) 当这个矩阵不满秩，则意味着其对应的线性方程组有多个解，我们需要在这些解中选择一个作为输出。一种简单的方法是添加正则项，从而抑制绝对值过大的参数。关于正则化，我们留到以后讨论。

重量(x_1)	店家(x_2)	价格(y)
100	1	25
200	1	35
300	1	45
50	2	20
150	2	32
250	2	39
350	2	51
99	3	25
199	3	35
299	3	44
399	3	53

我们将数据集稍微扩展一下，加入了店家的因素。由于店家是离散的标号而不是一个定值，我们需要使用 one-hot 编码来对其进行处理。One-hot 编码的表现方式如下：

店家1: [1, 0, 0]
店家2: [0, 1, 0]
店家3: [0, 0, 1]

可以看出，one-hot 编码的本质可以看做是在运算的时候，根据离散特征的不同取值，抽出不同的权重输入模型。比起直接输入 1, 2, 3 这样的序数， one-hot 编码可以完全避免序数的取值所造成的影响，同时由于每个离散值都有不同的权重，可以更好地表达离散特征的特点。
我们的数据变为这个样子：

重量(x_1)	店家(x_2)	价格(y)
100	1, 0, 0	25
200	1, 0, 0	35
300	1, 0, 0	45
50	0, 1, 0	20
150	0, 1, 0	32
250	0, 1, 0	39
350	0, 1, 0	51
99	0, 0, 1	25
199	0, 0, 1	35
299	0, 0, 1	44
399	0, 0, 1	53

解得各项权重为：
0.20509679 , -11.4375, 6.75, -23.9375, 27.3125

观察中间三项代表每个商家的权重，我们可以发现，第二家店([0, 1, 0])的权重最大，
意味着其具有最高的性价比。

线性分类

在上面，我们用线性模型处理了用于预测价格的回归问题。而对于你来说，你还有一个更加关心的事情—如何用线性回归决策史莱姆在战斗中的行为？

你能够命令史莱姆在战斗中做的行为有两种：攻击与防御。你希望让史莱姆在对手弱小，自己状态好的时候尽可能地多攻击，以加快打素材的效率；你又希望史莱姆在面对强敌，或者自己状态差时候尽可能多防御，从而不会拖累你的药品补给。从机器学习的角度来看，你希望得到这么一个模型函数 f(对方攻击，对方防御，自身血量，自身攻击，自身防御) = (攻击，防御)。

基于你对史莱姆行为的观察，

让我们回到线性模型上来。线性模型的目标是习得一条直线（在高维空间中，是一个平面或者超平面），而我们可以很直观地得出，这条直线能够将整个平面一分为二。套用到我们的学习目标上，我们可以这么叙述：我们希望学到一条直线能将由属性(对方攻击，对方防御，自身血量，自身攻击，自身防御)所组成的样本空间分成两个互补的部分（攻击，防御）。当面对新的情况时，预测值如果在攻击的一侧，则选择攻击；反之则选择防御。也就是说，当函数f的值大于（或等于）某个“阈值”的时候，选择攻击；而小于的时候选择防御。令 1 表示攻击，令 0 表示防御受：

$f(\mathbf{x}) = \mathbf{w}^T\mathbf{x} > \theta \rightarrow 1$
$f(\mathbf{x}) = \mathbf{w}^T\mathbf{x} <= \theta \rightarrow 0$

将阈值 $\theta$ 整合到左边的截距项并且用之前的常数项加常数输入化简成向量形式，定义0-1阶跃函数 $l_{0/1}(z) = 0 if z <= 0 else 1$ 。我们的线性分类函数重写为：

$f(\mathbf{x}) = l_{0/1}(\mathbf{w}^T\mathbf{x})$

但是，当你想跟回归模型一样求导取导数为零的时候，你发现了一个很严重的问题：阶跃函数的导数要么是0，要么不可导。这直接影响了求导的链式法则导致无法求导。有没有这样一个函数，它又能模拟阶跃函数的行为，又有良好的可导性呢？

你想到了 sigmoid 函数：

$\sigma(z) = \frac{1}{1+e^{-z}}$

这个函数有几个很好的特性：

原来线性模型的值域范围是整个实数集 R，而 sigmoid 函数将整个实数集映射到 (0, 1)范围内。
这个函数处处可导，从而避免了阶跃函数无法求导，不能应用链式法则的尴尬。
sigmoid 函数有很好的可解释性。

对 sigmoid 函数求导：

$\begin{aligned} \sigma'(z) &= \frac{\partial \sigma}{\partial z} \\ &= \frac{1' * (1+e^{-z}) - 1 * (1+e^{-z})'}{(1+e^{-z})^2}\\ &= \frac{e^{-z}}{(1+e^{-z})^{2}} \\ &= \frac{1}{1+e^{-z}}\frac{(1+e^{-z})-1}{1+e^{-z}}\\ &= \frac{1}{1+e^{-z}}(1 - \frac{1}{1+e^{-z}})\\ &= \sigma(z)(1 - \sigma(z)) \end{aligned}$

另一方面，将 $z=\mathbf{w}^T\mathbf{x}$ 代入，然后变形。令 $y=\sigma(\mathbf{w}^T\mathbf{x})$ ：

$\begin{aligned} y &= \frac{1}{1+e^{-\mathbf{w}^T\mathbf{x}}}\\ y + ye^{-\mathbf{w}^T\mathbf{x}} &= 1\\ e^{-\mathbf{w}^T\mathbf{x}} &= \frac{1-y}{y} \\ -\mathbf{w}^T\mathbf{x} &= \ln\frac{1-y}{y}\\ \mathbf{w}^T\mathbf{x} &= \ln\frac{y}{1-y} \end{aligned}$

我们可以将项 $y/(1-y)$ 看做样本决策为正与样本决策为负的概率的比值。由于 sigmoid 函数的值域在 $(0,1)$ ，我们可以将其看做给定样本值，决策为正的条件概率, 1-sigmoid 为决策为负的概率。对上式，我们将其重写为：

$\ln\frac{Pr\{y=1 | \mathbf{x}\}}{Pr\{y = 0 | \mathbf{x}\}} = \mathbf{w}^T\mathbf{x}$

也就是说，我们希望习得的分类线实际上代表了正类与负类的概率的比。

由于我们有了一个很好的概率解释，我们可以通过极大似然法来对参数向量 w 进行估计：我们认为，最优的分类器必然能够使得数据集上的样本“最可能”被分类为正确的类别。换句话说，如果一个样本在数据集中标记为正，则我们学习的模型将有更大的可能性输出高概率；反之则输出低概率。对于整个训练集而言，我们希望最大化整体的分类概率：

$P(\mathbf{w}) = \prod_i^N Pr\{y=y_i | \mathbf{x};\mathbf{w}\}$

对数化处理让连乘变为连加：

$\ln P(\mathbf{w}) = \sum_i^N \ln Pr\{y=y_i | \mathbf{x};\mathbf{w}\}$

我们的损失函数叫做对数似然函数：

$\max_\mathbf{w} J(\theta=\mathbf{w}) = \ln P(\mathbf{w})$

而线性分类模型被称作“对率回归模型”（逻辑回归模型），虽然它是一个分类模型。我们定义我们的机器学习任务如下：

输入特征：对方攻击，对方防御，自身血量，自身攻击，自身防御……
输出标签：攻击(正)，防御(负)
学习器：对率回归模型
损失函数：对数似然函数
优化器：在这个阶段，你决定先用手动调节的方式进行调参。

由于 $Pr \{y=y_i|\mathbf{x}; \mathbf{w}\}$ 这一项现在是概率形式，我们要将其转化为具体的表达方式。这里有一个 trick: 由于 $y$ 的取值只有 0 与 1，当 $y=0$ 的时候， $1-y$ 等于1。

当 $y=1$ 的时候，我们关注样本被分类为正的概率 $\sigma(\mathbf{w}^T\mathbf{x})$
当 $y=0$ 的时候，我们关注样本被分类为负的概率 $1-\sigma(\mathbf{w}^T\mathbf{x})$

基于这两个观察，我们用 $y$ 与 $1-y$ 作为指示器：

$Pr\{y_i | \mathbf{x}; \mathbf{w}\} = (1-\sigma(\mathbf{w}^T\mathbf{x}))^{y} \sigma(\mathbf{w}^T\mathbf{x})^{1-y}$

当样本是正类时，正概率起作用；当负类时则反之。

于是我们的对数似然函数就变成了：

$\begin{aligned} J(\mathbf{w}) &= \sum_i^N\ln ( \sigma(\mathbf{w}^T\mathbf{x})^{y_i}(1-\sigma(\mathbf{w}^T\mathbf{x}))^{1-y_i})\\ &= \sum_i^Ny_i\ln \sigma(\mathbf{w}^T\mathbf{x})+(1-y_i)\ln (1-\sigma(\mathbf{w}^T\mathbf{x})) \end{aligned}$

优化器：梯度下降法

当然，我们希望同优化线性回归模型一样来优化对率回归模型。我们先对损失函数求导看看能不能找到解析解：

$\begin{aligned} \frac{\partial J}{\partial\mathbf{w}} &= \sum_i^N y_i \mathbf{x}_i \sigma(1-\sigma) \frac{1}{\sigma} + (1-y_i)\mathbf{x}_i\frac{1}{1-\sigma}(-\sigma)(1-\sigma)\\ &= \sum_i^N y_i \mathbf{x}_i (1-\sigma) - (1-y_i)\mathbf{x}_i\sigma\\ &= \sum_i^N (y_i -\sigma(\mathbf{w}^T\mathbf{x}))\mathbf{x}_i \end{aligned}$

显然由于只有当 $\sigma(\mathbf{w}^T\mathbf{x})$ 等于 $y_i$ 的时候或者 x 为零向量的时候可以得到极值，但是这是不可能的：首先，由于 sigmoid 函数的特性，其输出值要等于 1 或者 0 的时候我们需要 $\mathbf{w}^T\mathbf{x}$ 为正负无穷；其次，当 x 为零向量，sigmoid 的函数值为 0.5，对此我们无法进行有效分类。而对于实际应用而言，我们不需要一个完美的模型，我们只需要模型的误差在容忍范围内即可（考虑到过拟合问题，我们实际上不应该寻求一个完美的模型）。

我们可以用梯度下降法(gradient descent)来优化模型。想象一下爬山，当一只肥宅气喘吁吁爬到半山腰一脚踩空滚下去的时候(没有针对肥宅的意思，肥肥贴贴)什么时候能最快到坡底呢？肥宅滚下去的方向一定是最陡峭的方向。用数学语言说，就是瞬时变化率最大的方向。我们把表示这个方向的向量称作梯度。梯度是各维度偏导数在该点的值所组成的向量:

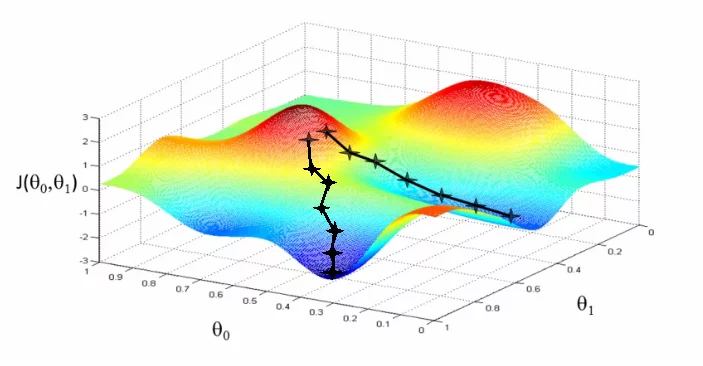
$\nabla f(\mathbf{x})= \frac{\partial f}{\partial x_1}\vec i_1 + \frac{\partial f}{\partial x_2} \vec i_2 ...$

梯度指向函数增长最快的方向，当我们需要最快到达底部时，我们要让权重朝梯度的反方向移动。由于函数的梯度方向在各点不一定一致，所以我们每次只能前进一小步，然后修正方向直到最底端。这个步长被称作学习率，用 $\eta$ 来表示。梯度下降法的算法如下：

while stopping criteria:
    $$w <- w - \eta \Nabla J$$

算法停止的条件，一般可以使用在测试集上的表现进行判断：当在测试集上计算的损失函数值不再改变或者改变量很小的时候，就可以停止算法进行输出；也可以指定循环个数，然后输出表现最好的权重。

由于对于梯度的计算使用了整个数据集，每次更新梯度都需要对整个数据集进行计算，这导致了我们的算法会变得很慢。解决的方法，有随机梯度下降(stochastic gradient descent) 与批量梯度下降(batch stochastic gradient descent)~~不要随便透~~两种。随机梯度下降指的是，每次从数据集中抽取一条数据计算损失函数的梯度，进行更新。批梯度下降介于随机梯度下降与全数据集梯度下降之间，每次抽取“一批”数量的数据进行梯度下降。这三者的期望相同，意味着只要运行足够长的时间，这三个算法都会收敛到同一个极小点。其中，随机梯度下降由于每次只选用一个数据进行计算，噪音比较大，下降的过程会比较“波折”。而批量梯度下降是效率与稳定性的折中，更加实用。

非线性问题的处理

线性模型有一个弱点体现在它的名字里面：对于非线性问题，单纯的线性模型没有很好的解决方案。
举个例子，线性模型对 XOR 没有很好的处理方案：

真值表	x1	x2
x1	0	1
x2	1	0

在二维空间，这四个点为：-(0,0), +(0,1), +(1,0), -(1,1)。
我们很难找到一个线性函数很好地将这四个特征点分开。但是如果我们能将其映射到三维空间，这四个点变为：
-(0,0,0), +(0,1,0), +(1,0,0), (-1,1,1)。
可以看出，在三维空间，我们可以找到一个平面将这四点正确地分开。这启发了我们：诸如二次函数这种在低维空间是非线性的数据，在高维空间有可能能够用线性模型进行处理。我们令这个到高维的映射为 $\mathbf{\phi}$ ，线性模型变为如下形式：

$f(\mathbf{x}) = \mathbf{\phi}(\mathbf{w})^T\mathbf{x}$

其中， $\phi$ 的映射用向量形式表示为：

$\mathbf{\phi}(\mathbf{x}) = [\phi_1(\mathbf{x}), \phi_2(\mathbf{x}) ... \phi_K(\mathbf{x})]^T$

这样的函数我们称为基函数。一般而言，常用的基函数有：

多项式： $(x_1, x_2...x_n)$ => $(x_1^2, x_1x_2, ... x_2x_1, x_2^2, x_2 x_3,...$
径向基函数(RBF)，这是一种类似于高斯函数的函数: $\exp(-(\mathbf{x} - \mathbf{c})^T(\mathbf{x}-\mathbf{c})/h^2$
logisitic-sigmoid 函数： $1/(1+\exp(-\mathbf{v}^T\mathbf{x}-b))$

下图我们简单地使用了多项式基函数，可以看出其对一条三次曲线的拟合效果是比较好的，而单纯的线性回归显然不符合实际。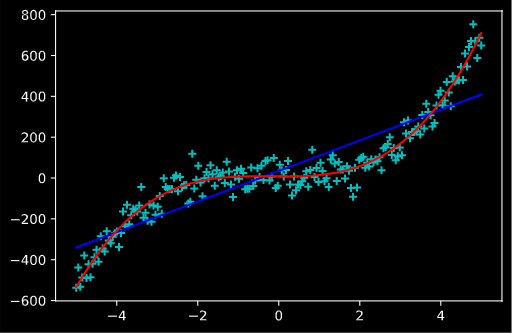

下图使用了 RBF 基函数来拟合一条噪音比较大的四次曲线，效果与多项式类似。

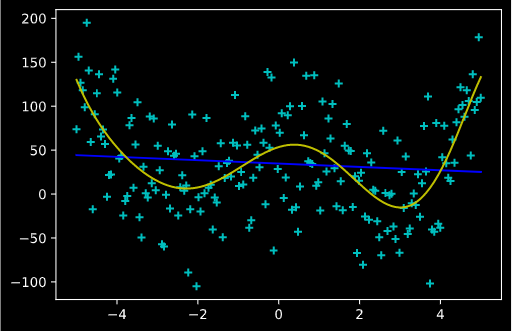
但是，由于基函数的参数(多项式的次数，RBF的带宽与中点等)是手工调整的，我们需要注意这些参数如果不加注意，会给我们带来麻烦。典型的问题就是过拟合 (overfitting)。当多项式的次数过高，或者 RBF 的带宽过小（想想为什么！），函数拟合曲线的能力就会过强，导致在训练集上几乎能拟合每一个点，但是在训练集上效果就很差。下图是一个多项式基函数次数过高的曲线，可以看出其拟合出一条连接每一个数据点的折线, 但是这个折线在未来的测试集上就可能出现偏差。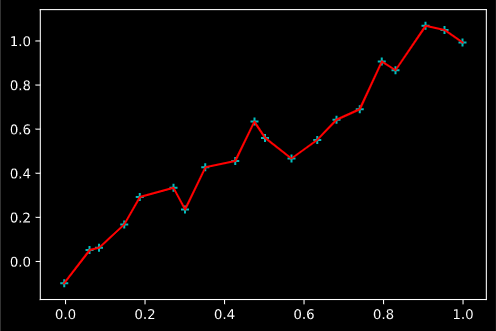

后记

废了九牛二虎之力，你终于调教出了一只能够帮助你攻击的史莱姆。但是你的生活并没有多少改变：依旧过着拳打南山哈比幼儿园，脚踢北海哥布林敬老院的生活。你的史莱姆大概帮你提高了 10% 的打素材效率，但是打不过的怪还是打不过，依旧处于鄙视链的最底层。

但是，照这个趋势下去，你也总是能攒下一笔小钱用于更新装备了。虽然不能从此出任 CEO 赢娶白富美走上人生巅峰，只要有了钱，就有了生存下去的希望。看着战斗中奋力扭动的史莱姆，你这么想着：“我也事加把劲骑士了!”

To be continued…

重量(x_1)	店家(x_2)	价格(y)
100	1	25
200	1	35
300	1	45
50	2	20
150	2	32
250	2	39
350	2	51
99	3	25
199	3	35
299	3	44
399	3	53

重量(x_1)	店家(x_2)	价格(y)
100	1	25
200	1	35
300	1	45
50	2	20
150	2	32
250	2	39
350	2	51
99	3	25
199	3	35
299	3	44
399	3	53

穿越到异世界的魔物使生活：线性模型