开始认真刷西瓜书了，作为面试的准备。规划是重点公式+有价值的练习题推一遍或者编程实现，由于同时也要刷 leetcode 与找内推所以更新不定。本文会包括 1-2 章的内容以及习题。

一些碎碎念：之前跟朋友聊的时候说到在瓶颈期要保持产出——不论是知识还是产品，那么现在姑且就把知识整理一下吧，虽然做的有点晚，但是总比不做好。博客改成hexo以后好多以前的文章暂时没空搬过来，可能要留到以后整理了，因为好多图放在七牛但是七牛现在对未备案域名有限制所以全挂了，怎么处理得慢慢来了。

迁移到hexo的时候也有好多坑，可能另外有空说一下，包括但不限于 Mathjax 引入，代码高亮，分享……（想在leancloud注册账号，要人脸认证但是我手机不给认证……）等。而且实际上主题没写完，手机端的样式没仔细调，一些页面的样式没写，等等。但是毕竟是从头写起的一个主题，拖延了好久的想法终于实现80%，感觉还是不错的。

第一章绪论

一些基本概念的定义

机器学习：使用计算的手段，利用经验改进自身性能。
模型：从数据中学的的结果。模型习得的是关于规律的一个假设 (hypothesis)，真实的规律被称为 ground truth
数据集：数据的集合，每条记录是一个样本。也有认为数据集是一个对整个样本空间进行采样的样本。
特征向量：样本对应的属性的向量化，表示为特征空间的一个向量。
分类：预测值为离散值
回归：预测值为连续值
训练集，测试集: 训练集用于学习模型，测试集用于测试模型的性能
有监督学习：训练集上的样本给定标记信息
无监督学习：训练集上的样本无标记信息或者监督信息
泛化：学习的模型在未见过的样本上的适应能力
假设空间：所有可能的假设（模型）所组成的空间，学习的过程可以看做是在假设空间中搜索一个最适用的模型的过程
版本空间：与训练集一致的假设集合

归纳偏好

由于训练集只是样本空间的某些采样的集合，仅仅依赖训练样本我们可以训练出若干个模型，但是没有办法判断哪种模型更好。为了选出更优的模型，我们会对某些类型有一些偏好（比如泛化能力等），这种偏好叫做假设偏好。

根据假设偏好，我们能够选出更优的模型；但是只有当假设偏好于问题匹配的时候，我们才能根据假设偏好选择出更适用于实际问题的模型。
根据“没有免费午餐”定理（证明见书），在真实目标函数是均匀分布的情况下，任何学习算法的期望性能都相同。换言之，讨论学习算法的性能与好坏必须基于实际问题，归纳偏好一定要与实际问题相符才能得出正确的结论。

机器学习的发展历史略。

习题

西瓜数据集

先给出西瓜数据集1.1：

编号	色泽	根蒂	敲声	好瓜
1	青绿	蜷缩	浊响	T
2	乌黑	蜷缩	浊响	T
3	青绿	硬挺	清脆	F
4	乌黑	稍卷	沉闷	F

从表中我们得到

特征空间：
1.色泽：青绿、乌黑
2.根蒂：蜷缩、硬挺、稍卷
3.敲声：浊响、清脆、沉闷
标记空间：
- 好瓜：T、F

习题及解答

1.1 表中若只包含1， 4两个样例，求版本空间

假设空间的大小为每个属性的取值数 +1 （泛化在所有取值的操作符 *) 的连乘+1 再加上空集（即概念无效）

$1 + \prod_{k=1}^K (\#k+1)$

我们要做的是两步:

删除不包含数据1（正例）的假设
在上一步的基础上删除包含数据1与数据4的假设

结果如下：

青绿，蜷缩，浊响(均无泛化的情况下，有唯一正例)
青绿，蜷缩，\*；青绿，\*，浊响；\*，蜷缩，浊响(一个泛化)
青绿，\*, \*；\*, 蜷缩, \*；\*, \*, 浊响(两个泛化)

排除空集（有正例）与全部泛化（有反例）

1.2 用析合范式表示数据集1.1的假设空间，计算可能的假设数，析合范式包含 k 个合取式

首先，基于数据集我们可以计算出合取式的假设空间 (k=1) 为 3 * 4 *4 + 1 = 49

以下讨论定义 $\#$ 为计数函数。

单独处理空集，取消空集后的选择数为 $N = C_{48}^k$ ，加上空集的组合为 $2N+1$(所有组合都可并一个空集，加上单独的空集自身)
对三个属性泛化的表达式 A = (a=*, b=*, c=*) 与其他所有的泛化式均有：(A or B) = A，即 $C_{47}^{k-1}$
对两个属性泛化的表达式形如 A = (a=0, b=*, c=*)，重复的冗余形如 B = (a=0, b=1, c=*)。我们可以删除一个属性，A' = (b=*, c=*)求其所有可能的泛化组合： $C_{\#_b\times\#_c+1}^{k-1}$ ，b, c 为非a的属性。两个属性的泛化表达式一共有 $\sum_i \#_i$ 种。
对一个属性泛化的表达式形如 A = (a=0, b=1, c=*)，重复的冗余形如 B = (a=0, b=1, c=2)。其泛化组合即为 $C_{\#c}^{k-1}$ ，一共有 $\sum_i \#_a \#_b$ 种，其中a, b为非泛化的属性。
补集的情况不知道是不是算冗余，如果是的话情况会比较复杂，会跟k有关。

这里有一个编程实现，应当是考虑了补集的。

1.3 若数据包含噪声，设计一种归纳偏好

简单地说，特征类似应当具有类似的输出，但是这个要具体问题具体分析（反例：特征工程做得不好，有很多无效的特征,e.g. 特征向量维度 100 但是实际有用的维度只有1，此时这个归纳偏好就不太好）。

1.4 用其他性能度量证明没有免费午餐定理

TODO

第二章模型评估与选择

经验误差与过拟合

对于分类任务而言，若样本数为 m，分类错误数为 a，则错误率定义为 $E=a/m$ ，精度为 $A = 1-E$ 。更一般的，我们将实际预测输出与样本真实输出的差异称作误差。在训练集上的误差为训练误差或者经验误差(training error)，在新样本上的误差为泛化误差(generalization error)。

过拟合指的是学习器在训练样本上学习的“太好”，以至于在非训练样本上表现的不好，即泛化误差大于训练误差。欠拟合指的是在训练样本上没有恰当地学习到模型。在真实的任务中，欠拟合比较少见而过拟合比较多见，所以我们通常集中于讨论如何避免过拟合。

测试集及其划分

测试集通常用于判断样本的泛化能力。给定有 m 个数据的数据集 D，我们将其划分为测试集 T 与训练集 S。一般而言划分有如下方法：

留出法：直接将数据集划分成两个互斥集合。我们在划分数据集的时候通常需要保证数据分布的一致性，避免划分的偏差影响结果。另外，测试集过小会导致测试结果不够稳定准确，测试集过大会导致学习的模型的性能不够好。一般而言训练集占比为 2/3 到 4/5。
交叉验证(cross validation) 将数据集先划分为 k 个互斥子集，对于每个子集尽量保持数据一致性；然后抽出一个作为测试集，剩余的合并成为训练集，从而进行 k 次训练。结果是这 k 次的均值。特例：留一法：子集的粒度划分到每一个样本。其好处是，评估的效果会跟真实效果比较接近；坏处是计算量偏大。
自助法(bootstrapping): 留出与交叉验证都会引入一些根据数据分布的不稳定因素，留一法能够最大程度上减小这种估计偏差但是计算量太大。自助法以自助采样为基础，给定大小为 m 的数据集 D，每次随机挑选一个样本放入采样数据集 D’。执行 m 次后我们获得了一个包含 m 个样本的数据集 D’。样本不被采集到的的概率为1-(1/m)^m，取 m 趋于无穷的极限得到大约有 1/e (36.5%)的样本不被采集到。于是我们可以将 D’ 用作训练集， D - D' 用作测试集。自助法用于数据比较小的情况，而且自助法能够产生不同的数据集，对集成学习有好处；但是对初始数据集分布的改变也会引入偏差，因此在数据集足够的时候用的比较少。

性能度量

均方误差，精度与错误率

如上文所述，分类任务通常使用错误率与精度来衡量学习器的性能。对于回归任务而言，常用的性能度量是均方误差(mean square error)：

$E(f;D) = \frac{1}{m} \sum_{i=1}^m (f(\mathbf{x}_i)-y_i)^2$

其积分形式可以用于描述更为一般的数据分布:

$E(f;\mathcal{D}) = \int_{x\sim \mathcal{D}} (f(\mathbf{x}) - y)^2p(\mathbf{x})d\mathbf{x}$

类似的，分类错误率定义为：

$E(f;D) = \frac{1}{m} \sum_{i=1}^m \mathbb{I}(f(\mathbf{x}_i) \neq y_i)\\ E(f;\mathcal{D}) = \int_{x\sim \mathcal{D}} \mathbb{I}(f(\mathbf{x}) \neq y)p(\mathbf{x})d\mathbf{x}$

精度定义为：

$E(f;D) = \frac{1}{m} \sum_{i=1}^m \mathbb{I}(f(\mathbf{x}_i) = y_i)\\ E(f;\mathcal{D}) = \int_{x\sim \mathcal{D}} \mathbb{I}(f(\mathbf{x}) = y)p(\mathbf{x})d\mathbf{x}$

混淆矩阵与F1 score

单单使用精度或者错误率不能满足所有任务需求。我们通常用查准率，查全率与 F-1 score 来更全面地描述学习器的性能。
对二分类任务，我们有真正例(TP)，假正例(FP)，真反例(TN)，假反例(FN)四种情况，如下即为相关的混淆矩阵：

真实/预测	正例	反例
正例	TP	FN
反例	FP	TN

我们定义查准率 P 与查全率 R:

$P = \frac{TP}{TP+FP}\\ R = \frac{TP}{TP+FN}$

查准率-查全率是有一定矛盾的，希望查准率高，就会尽可能地减少数量，这就会导致查全率变少；提高查全率则反之。为了更全面地比较，我们可以画出P-R曲线图。一般曲线能够完全包住另一个学习器的情况，就说明该算法较优。另一方面，F-1 score 是另一种结合上述两种度量的性能度量

$F1 =\frac{2PR}{P + R}$

对于多次训练/多个数据集的情况，我们通常对一次训练计算一次混淆矩阵，然后求全局的平均P, R 值，再计算全局的 F1 score。

ROC, AUC

考虑这样一种分类器：其输出值是 0-1 之间的实数，我们设定一个分类阈值，比如 0.5，来决定输出的标签是正类还是反类。我们可以将样本按照输出值进行排序。如果不考虑阈值，这个实值的好坏决定了分类器的好坏：如果这个值分的更开，说明分类越好。我们可以直观的理解其下界：以均匀分布随机输出实值。在这个排序中，调整截断点的位置可以体现对 P 或者 R 的重视程度，而排序本身体现了期望泛化性能的好坏。

ROC 曲线就是一种应用了这种思想的曲线，纵轴是真正例率(TPR)，横轴是假正例率(FPR)。其计算如下：

$TPR = \frac{TP}{TP+FN}\\ FPR = \frac{FP}{TN+FP}$

类似的，我们可以与P-R曲线一样判断 ROC 曲线下学习器的优劣：能够全包的曲线一般更优。在没有办法全包的情况，我们一般计算曲线包围的面积 AUC。由于我们一般在离散的样本上进行学习测试，其曲线也是曲折的，我们用一个个小矩形来近似 AUC:

$AUC = \frac{1}{2}\sum_{i=1}^{m-1}(x_{i+1} - x_i)(y_i + y_{i+1})$

代价敏感错误率与代价曲线

现实中不同类型的错误造成的后果不同：比如在医疗诊断中，将患者诊断为健康可能造成不可控的后果，但是将健康人诊断为患病的后果就相对比较小。为了权衡不同类型错误的损失，可以为错误赋予非均等代价。我们可以设定代价矩阵：

真实类别/预测类别	第0类	第1类
第0类	0	c01
第1类	c10	0

我们可以计算代价敏感错误率，令 $D^+$ , $D^-$ 分别为正，反例子集：

$E(f;D; c) = \frac{1}{m} (\sum_{\mathbf{x}_i \in D^+}\mathbb{I}(f(\mathbf{x}_i \neq y_i))\times c_{01}\\ + \sum_{\mathbf{x}_j \in D^-}\mathbb{I}(f(\mathbf{x}_j \neq y_i)) \times c_{10})$

在非均等代价下， ROC 曲线不能直接反映期望总体代价，我们使用代价曲线来取代。其横轴为 $[0,1]$ 的正例概率代价

$P(+)cost = \frac{p\times c_{01}}{p\times c_{01} + (1-p)\times{c10}}$

取 $p$ 为正例概率。纵轴是取值为 $[0,1]$ 的归一化代价：

$c_{norm} = \frac{FNR\times p \times c_{01} + FPR\times(1-p) \times c_{10}}{p\times c_{01} + (1-p)\times c{10}}$

在ROC曲线上，每一点的坐标是(TPR, FPR)。我们可以计算出假反例率 FNR=1-TPR，从而可以在代价敏感图中画出一条从(0, FNR) 到 (1, FPR) 的线段，所有线段的下界包起来的面积即为期望总体代价。

比较检验

我们通常用测试集上的某些性能度量来衡量学习器的性能，但是：

泛化性能跟测试集上的性能未必相同
测试集的性能跟测试集自身的选择密切相关
算法本身的随机性导致测试集上的性能未必相同

基于这些问题，我们使用统计假设检验(hypothesis test)帮助我们比较学习器的性能。假设检验能让我们推断出，如果测试集上观察到某个学习器A比学习器B优，那么 A 泛化性能是否比 B 好，以及该结论把握多大。根据知乎的解释，西瓜书这里的公式2.27有误，正确的推理如下：

令泛化错误率为 $\epsilon$ , 测试错误率为 $\hat \epsilon$ 。在测试集上，恰有 $\hat\epsilon\times m$ 个样本被误分类。根据泛化错误恰好将测试集上错误分类的概率为：

$P(\hat\epsilon;\epsilon) = \begin{pmatrix}m\\ \hat\epsilon \times m\\ \end{pmatrix} \epsilon^{\hat\epsilon\times m}(1-\epsilon)^{m-\hat\epsilon\times m}$

当测试错误率与泛化错误率相等时， $P$ 最大。考虑假设 $\epsilon < \epsilon_0$ （泛化错误率小于某个阈值）。
原假设 $H_0: \epsilon \leq \epsilon_0$ ，备择假设 $H_1: \epsilon>\epsilon_0$ 。

若原假设成立，那么采样测试错误率小于某个临界值 $\hat\epsilon \leq \overline \epsilon$ 。从条件概率的角度理解： $P(\hat\epsilon \leq \overline \epsilon |H_0) >= 1-\alpha$ 。等价于 $P(\hat\epsilon \gt \overline \epsilon | H_0) < \alpha$ 。其中， $1-\alpha$ 为置信度，意思即为原假设成立的概率。

我们需要计算这个观测临界值 $\overline\epsilon$ 。考虑西瓜书图2.6类似的概率分布，误分类样本为右侧的阴影表示。这个概率分布表示所有可能的误分类数发生的概率。想象在概率分布图上画一根竖线分割概率密度函数曲线为两个部分，右侧为小概率事件发生，需要拒绝原假设（拒绝域）；左侧为大概率事件发生，接受原假设（接受域）。这条线 $0 < l < 1$ 是接受域的上限，拒绝域的下限。我们需要拒绝域的面积最大为 $\alpha$ ，则我们需要寻找一个最小的 $l$ ，使得右边阴影面积最大为 $\alpha$

$\overline\epsilon = \min \epsilon~s.t. \sum_{i=\epsilon\times m+1}^{m} \begin{pmatrix}m\\ i \\ \end{pmatrix}\epsilon_0^i(i-\epsilon_0)^{m-i} < \alpha$

这个 $\overline\epsilon$ 就是我们的接受域上界。

t检验

我们对使用交叉验证或者多次重复留出法可以得到多个测试错误率，此时可以使用 t 检验。首先计算平均错误率与方差：

$\mu = \frac{1}{k} \sum_{i=1}^k \hat\epsilon_i\\ \sigma^2 = \frac{1}{k-1} \sum_{i=1}^k(\hat\epsilon_i - \mu)^2$

我们将其看做是对泛化错误率的独立采样:

$\tau_t = \frac{\sqrt{k}(\mu - \epsilon_0)}{\sigma}$

这个统计量服从于自由度为 $t-1$ 的 t 分布。类似的，左右两边的阴影大小分别应该为 $\frac{\alpha}{2}$ 。如果平均错误率与 $\epsilon_0$ 之差在分布的中间，则可以接受原假设。

交叉验证t检验

我们对 A, B 两个学习器分别求 k-fold 交叉验证，得到两组错误率；同时，我们又可以得到两组错误率之差。因此，我们可以对这两组错误率之差做 t 检验。计算差值的平均值与方差，令变量 $\tau_t = |\frac{\sqrt{k}\mu}{\sigma}|$ 。我们将原假设设为两个学习器的性能没有区别，用类似的方法来处理这个变量，以判断是否接受原假设。

McNemar 检验

对于二分类问题，我们有两个学习器A，B，不仅可以计算其错误率，也可以计算其分类结果的差别：

B/A	正确	错误
正确	e00	e01
错误	e10	e11

如果我们假设两学习器性能相同，则e01 = e10，那么 |e01 - e10| 应服从正态分布，均值为1，方差为 e01+e10。令变量

$\tau_{\chi^2} = \frac{(|e_{01} - e_{10}|-1)^2}{e_{01} + e_{10}}$

服从于自由度为1的卡方分布。

Friedman 检验 Nemenyi检验

见书，感觉用的不是很多，要用的时候查一下吧。
F检验大致的思想：对各个算法在不同数据集上的性能进行排序，如果他们性能相同，那么他们的平均序值应当相同。
如果其性能不相同，那么我们可以用 Nemenyi 后续检验来进一步区分各个算法：给出一个临界值，如果两个算法平均序值之差超过临界值，则拒绝两个算法性能相同这一假设。

偏差与方差

偏差-方差分解是一个比较重要的工具。给定数据集 D 学习器 f, 对测试样本 x，令 yd 为数据集中的标记，y 为真实标记。
对于回归任务，学习算法的期望预测：

$\hat f(\mathbf{x}) = \mathbb{E}_D[f(\mathbf{x}; D)]$

样本相同，不同的训练集产生的方差为：

$var(\mathbf{x}) = \mathbb{E}_D[(f(\mathbf{x};D)-\hat f(\mathbf{x}))^2]$

噪声为

$\epsilon^2 = \mathbb{E}_D[(y_D - y)^2]$

期望输出与真实标记之间的差别称为偏差(bias)：

$bias^2(\mathbf{x}) = (\hat f(\mathbf{x}) - y)^2$

推导过程见书，从期望泛化误差开始推导。我们证明泛化误差可分解为偏差，方差与噪声之和。
偏差度量学习器输出与真实的偏离程度，即算法本身的拟合能力；方差度量同样大小的训练集变动所导致的学习性能变化，即数据扰动的影响；噪声定义了期望泛化误差的下界。这意味着泛化性能由学习器本身的学习能力，数据的充分性与学习任务本身的难度共同决定。

一般而言方差与偏差是有冲突的，训练不足，学习器拟合能力不强，偏差主导对泛化性能的影响；训练充分，学习能力足够强，训练数据的扰动被学习器习得，从而方差的影响程度逐步加深；当训练过拟合，数据的微小扰动都会导致方差的巨大变化。

习题

1000个样本, 500正例500反例。划分为包含70%的训练集与30%的测试集用于留出法评估，估算划分方式

没有额外信息，我们保证正例跟反例在训练集跟测试集里的比重相等。

$C_{500}^{350} \times C_{500}^{350}$

100个样本，正，反例各一半，假定学习算法的新模型是将新样本预测为训练样本较多的类。给出用10折交叉验证与留一法分别对错误率进行评估所得的结果

10折：理想情况下正，反例在整个数据集与每个fold的分布都是均匀的，错误率期望是 50%
留一法：每次取一个样本，剩下的样本会有49个同类，50个相反，错误率是100%

若学习器 A 的 F1 值比 B 高，求 A 的 BEP 值是否也更高

不一定，感觉这两个没有明确的关系，见知乎

真正例率，假正例率，查准率，查全率之间的关系

$TPR = \frac{TP}{TP + FN}\\ FPR = \frac{FP}{FP+TN} \\ P = \frac{TP}{TP+FP} \\ R = \frac{TP}{TP+FN} \\$

显然，TPR = R

证明式 2.22

数学玩法参考这里

我们要证明的是：

$\mathcal{l}_{rank} = \frac{1}{m^+m^-} \sum_{\mathbf{x}^+\in D^+}\sum{\mathbf{x}^-\in D^-} (\mathbb{I}(f(\mathbf{x}^+)< f(\mathbf{x}^-))+ \frac{1}{2}\mathbb{I}(f(\mathbf{x}^+) = f(\mathbf{x}^-))) \\ AUC = 1 - \mathcal{l}_{rank}$

这里有比较详细的说明。

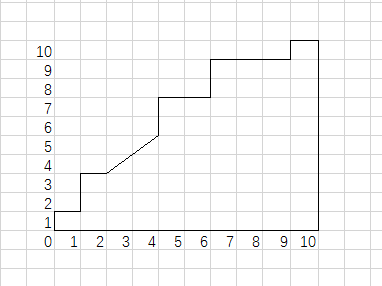
ROC_curve

如图，横轴纵轴分别被分割为 $1/m^-$ ， $1/m^+$ 的小条，划分出每个小块面积为 $1/m^-1/m^+$ 都代表一对样本对(a, b)。当 $f(a) > f(b)$ 且a为正例，b为反例的时候，这个方块在ROC曲线下方；当两者相等，则用一个占一半面积的三角形替代。于是损失函数等同于在上方的方块数+一半的边界三角形数乘以单位面积，即为ROC曲线上方的面积。

ROC曲线与错误率的关系

ROC曲线上每一点都对应一个错误率。
不考虑代价，我们有：

$E = \frac{FP+FN}{TP+FP+TN+FN}\\$

TPR, FPR见上。我们有

$FP = FPR \times (FP+TN)\\ FN = (1-TPR)\times(TP+FN)$

另外注意到FP+TN, TP+FN 分别为正例，反例的数量，所以我们可以得到

$E = (FPR \times m^- + (1-TPR)\times m^+)/ (m^+ + m^-)$

试证明任意一条ROC曲线都有一条代价曲线与之对应，反之亦然。

代价曲线是代价敏感图的下界，由于每一条代价线都是(0, FNR)到(1, FPR)的线段，而TPR=1-FNR，可以得出每一条代价线都能转换成(TPR, FNR)的形式，即ROC线上一点。由于代价曲线是这些线段族下确界组成的多边形，每个代价曲线都可以写成若干在ROC曲线上的点。反之，则可根据ROC曲线上的点做线段，取下界得到代价曲线。

min-max规范与z-score规范化的优缺点

min-max适用于规范化最大，最小值已知的情况，缺点是对极端数据敏感，出现极端数据需要取舍
z-score适用于未知的情况，或者有极端数据。另外数据归零化。缺点是计算量大，出现新数据要重新计算。

卡方分布检验过程，Friedman检验

略，不懂统计……

西瓜书笔记：1-2章(绪论，统计基础)

第一章 绪论